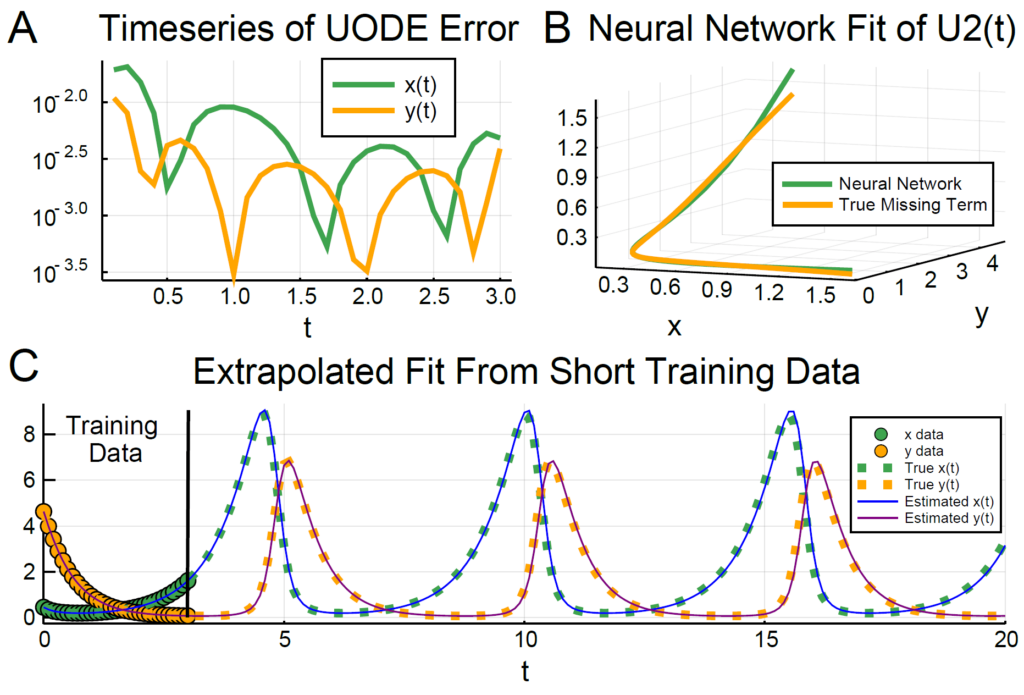
Neural Differential Equations (NDEs) have emerged as a powerful and versatile framework for modeling complex dynamical systems, making them well-suited for analyzing large-scale time series data in the realm of Big Data. By combining the principles of differential equations with neural networks, NDEs offer a flexible approach to capturing underlying patterns and dependencies within time series data. In this article, we will explore how to effectively implement NDEs for Big Data time series analysis, highlighting their potential applications, advantages, and best practices for handling massive datasets. Stay tuned to discover how NDEs can enhance the analysis and prediction capabilities for Big Data time series.
Understanding Neural Differential Equations
Neural Differential Equations (NDEs) combine the principles of neural networks with differential equations to model complex dynamic systems. The core idea is to use neural networks to parameterize the solutions of differential equations, enabling them to learn from data non-linearly. This approach is particularly powerful for analyzing big data time series due to its capability to capture temporal dependencies and model continuous-time processes.
Why Use Neural Differential Equations for Time Series Analysis?
The increasing volume and velocity of data generated across industries demand advanced analytical techniques. Traditional time series models often fall short in handling high-dimensional and large-scale datasets commonly encountered in big data. Neural differential equations offer several advantages:
- Flexibility: They can model complex nonlinear relationships.
- Scalability: Suitable for large datasets, thanks to their ability to interpolate and extrapolate from data efficiently.
- Continuity: They provide continuous-time modeling, which is ideal for irregular time series.
Setting Up Your Environment
Before diving into the implementation of neural differential equations, ensure you have the necessary libraries and tools installed. For a typical workflow, you will need:
pip install torch torchdiffeq numpy pandas matplotlib
The library torchdiffeq specifically provides functionalities to define and solve differential equations using PyTorch.
Data Preparation for Time Series Analysis
Proper data preparation is crucial for success in any big data analysis. The following steps guide you through this process when working with time series data:
- Loading the Data:
Utilize pandas to read your time series data from a CSV file or a database.
import pandas as pd data = pd.read_csv('your_data.csv') - Data Cleaning:
Handle missing values, outliers, and apply necessary transformations to normalize your data.
- Feature Engineering:
Create relevant features that could help the model learn better, such as lag features or rolling averages.
- Normalizing the Data:
Scale your data using Min-Max or Standard Scaler to ensure better convergence during training.
from sklearn.preprocessing import MinMaxScaler scaler = MinMaxScaler() scaled_data = scaler.fit_transform(data)
Building the Neural Differential Equation Model
Here, we define the structure of the neural differential equation model. We’ll use a simple ODE (Ordinary Differential Equation) parameterized by a neural network.
Defining the Neural Network
import torch
import torch.nn as nn
class ODEFunc(nn.Module):
def __init__(self, input_dim, hidden_dim):
super(ODEFunc, self).__init__()
self.fc1 = nn.Linear(input_dim, hidden_dim)
self.fc2 = nn.Linear(hidden_dim, input_dim)
def forward(self, t, x):
x = torch.relu(self.fc1(x))
x = self.fc2(x)
return x
Implementing the ODE Solver
To solve the differential equations, we use torchdiffeq, which provides various ODE solvers. You need to define the solver settings, including the time range and the initial conditions.
from torchdiffeq import odeint
def ode_model(t, x0):
ode_func = ODEFunc(input_dim=1, hidden_dim=50) # Modify as needed
return odeint(ode_func, x0, t)
Training the Model
Training a neural differential equation model involves minimizing the difference between the predicted and actual values. You can set up the training loop using PyTorch optimizers.
import torch.optim as optim
# Create the training loop
def train_model(data):
optimizer = optim.Adam(ode_func.parameters(), lr=0.01)
criterion = nn.MSELoss()
for epoch in range(1000): # Set number of epochs as needed
optimizer.zero_grad()
pred = ode_model(t_points, initial_conditions)
loss = criterion(pred, target_data)
loss.backward()
optimizer.step()
if epoch % 100 == 0:
print(f'Epoch {epoch}, Loss: {loss.item()}')
Making Predictions
After training your model, it’s time to make predictions on new, unseen data. Here’s how to perform predictions using your trained neural differential equation model:
with torch.no_grad():
future = ode_model(t_future, initial_conditions)
# Convert predictions back to original scale
predictions = scaler.inverse_transform(future.numpy())
Evaluating Model Performance
Once predictions are obtained, evaluating the model’s performance is essential. Common metrics for time series forecasting include:
- Mean Absolute Error (MAE): Average of the absolute differences between predictions and actual values.
- Root Mean Squared Error (RMSE): Square root of the average of squared differences.
- Mean Absolute Percentage Error (MAPE): Average of absolute percentage errors.
Implement evaluation metrics in Python:
from sklearn.metrics import mean_absolute_error, mean_squared_error
mae = mean_absolute_error(actual_data, predictions)
rmse = mean_squared_error(actual_data, predictions, squared=False)
print(f'MAE: {mae}, RMSE: {rmse}')
Visualization of Results
Visualizing the results helps in better understanding the model’s performance. Use matplotlib to plot the actual vs predicted values.
import matplotlib.pyplot as plt
plt.figure(figsize=(12, 6))
plt.plot(actual_data, label='Actual Data')
plt.plot(predictions, label='Predicted Data', linestyle='--')
plt.legend()
plt.title('Actual vs Predicted Time Series')
plt.show()
Challenges in Implementing Neural Differential Equations
While NDEs are powerful, several challenges must be navigated:
- Complexity: Designing, tuning, and interpreting neural differential equations can be more complex than traditional models.
- Computational Load: Training NDEs, especially on big data, may demand significant computational resources.
- Overfitting: With the flexibility of neural networks, overfitting is a risk. Regularization methods must be applied.
Best Practices for NDE in Big Data Contexts
To maximize the effectiveness of neural differential equations in big data time series analysis, consider the following best practices:
- Utilize appropriate data sampling techniques to manage large datasets without losing crucial information.
- Regularize your models with dropout layers or weight decay to prevent overfitting.
- Experiment with different architectures and hyperparameters for the neural network components.
- Monitor training in real-time to adjust parameters dynamically.
Additional Resources for Learning
For those interested in further exploring Neural Differential Equations, consider referring to the following resources:
- Research Papers: Look for the original paper on Neural ODEs by Chen et al. (2018).
- Online Courses: Platforms like Coursera and edX offer specialized courses on deep learning and differential equations.
- GitHub Repositories: Explore repositories related to neural differential equations for practical insights and implementations.
Implementing neural differential equations for Big Data time series analysis shows great promise in Revolutionizing the way we leverage Big Data for Time Series Analysis. By combining the power of neural networks with differential equations, we are able to effectively model and predict complex temporal patterns in large datasets, leading to more accurate and efficient analysis of Big Data time series. This approach holds significant potential for unlocking valuable insights and driving innovation in various industries that heavily rely on time series data analysis.